The 15 Hardest SAT MATH Questions

The 15 Hardest SAT Math Questions

.

No Calculator SAT Math Questions

Question 1

C=

5

9

(F−32)

The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?

1. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 

   5

   9

    degree Celsius.
2. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
3. A temperature increase of 

   5

   9

    degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

A) I only
B) II only
C) III only
D) I and II only

ANSWER EXPLANATION: Think of the equation as an equation for a line

y=mx+b

where in this case

C=

5

9

(F−32)

or

C=

5

9

F−

5

9

(32)

You can see the slope of the graph is 

5

9

, which means that for an increase of 1 degree Fahrenheit, the increase is 

5

9

 of 1 degree Celsius.

C=

5

9

(F)

C=

5

9

(1)=

5

9

Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of 

9

5

 degrees Fahrenheit.

C=

5

9

(F)

1=

5

9

(F)

(F)=

9

5

Since 

9

5

 = 1.8, statement II is true.

The only answer that has both statement I and statement II as true is D, but if you have time and want to be absolutely thorough, you can also check to see if statement III (an increase of 

5

9

 degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true:

C=

5

9

(F)

C=

5

9

(

5

9

)

C=

25

81

(whichis≠1)

An increase of 

5

9

 degree Fahrenheit leads to an increase of 

25

81

, not 1 degree, Celsius, and so Statement III is not true.

The final answer is D.

Question 2

The equation 

24x2+25x−47

ax−2

=−8x−3−

53

ax−2

 is true for all values of x≠

2

a

, where a is a constant.

What is the value of a?

A) -16
B) -3
C) 3
D) 16

ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by ax−2 (so you can get rid of the fraction). When you multiply each side by ax−2, you should have:

24x2+25x−47=(−8x−3)(ax−2)−53

You should then multiply (−8x−3) and (ax−2) using FOIL.

24x2+25x−47=−8ax2−3ax+16x+6−53

Then, reduce on the right side of the equation

24x2+25x−47=−8ax2−3ax+16x−47

Since the coefficients of the x2-term have to be equal on both sides of the equation, −8a=24, or a=−3.

The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.

The final answer is B.

Question 3

If 3x−y=12, what is the value of 

8x

2y

?

A) 212
B) 44
C) 82
D) The value cannot be determined from the information given.

ANSWER EXPLANATION: One approach is to express

8x

2y

so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting 23 for 8 in the numerator of 

8x

2y

 gives

(23)x

2y

which can be rewritten

23x

2y

Since the numerator and denominator of have a common base, this expression can be rewritten as 2(3x−y). In the question, it states that 3x−y=12, so one can substitute 12 for the exponent, 3x−y, which means that

8x

2y

=212

The final answer is A.

Question 4

Points A and B lie on a circle with radius 1, and arc 

⌢

AB

 has a length of 

π

3

. What fraction of the circumference of the circle is the length of arc 

⌢

AB

?

ANSWER EXPLANATION: To figure out the answer to this question, you'll first need to know the formula for finding the circumference of a circle.

The circumference, C, of a circle is C=2πr, where r is the radius of the circle. For the given circle with a radius of 1, the circumference is C=2(π)(1), or C=2π.

To find what fraction of the circumference the length of 

⌢

AB

 is, divide the length of the arc by the circumference, which gives 

π

3

÷2π. This division can be represented by 

π

3

*

1

2

π=

1

6

.

The fraction 

1

6

 can also be rewritten as 0.166 or 0.167.

The final answer is 

1

6

, 0.166, or 0.167.

Question 5

8−i

3−2i

If the expression above is rewritten in the form a+bi, where a and b are real numbers, what is the value of a? (Note: i=√−1)

ANSWER EXPLANATION: To rewrite 

8−i

3−2i

 in the standard form a+bi, you need to multiply the numerator and denominator of 

8−i

3−2i

 by the conjugate, 3+2i. This equals

(

8−i

3−2i

)(

3+2i

3+2i

)=

24+16i−3+(−i)(2i)

(32)−(2i)2

Since i2=−1, this last fraction can be reduced simplified to

24+16i−3i+2

9−(−4)

=

26+13i

13

which simplifies further to 2+i. Therefore, when 

8−i

3−2i

 is rewritten in the standard form a + bi, the value of a is 2.

The final answer is A.

Question 6

In triangle ABC, the measure of ∠B is 90°, BC=16, and AC=20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 

1

3

 the length of the corresponding side of triangle ABC. What is the value of sinF?

ANSWER EXPLANATION: Triangle ABC is a right triangle with its right angle at B. Therefore, AC is the hypotenuse of right triangle ABC, and AB and BC are the legs of right triangle ABC. According to the Pythagorean theorem,

AB=√202−162=√400−256=√144=12

Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle∠F equals the measure of angle∠C. Therefore, sinF=sinC. From the side lengths of triangle ABC,

sinF=

oppositeside

hypotenuse

=

AB

AC

=

12

20

=

3

5

Therefore, sinF=

3

5

.

The final answer is 

3

5

 or 0.6.

Calculator-Allowed SAT Math Questions

Question 7

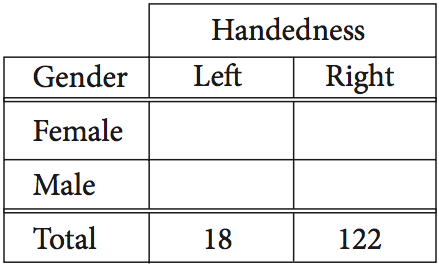
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. if there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)

A) 0.410
B) 0.357
C) 0.333
D) 0.250

ANSWER EXPLANATION: In order to solve this problem, you should create two equations using two variables (x and y) and the information you're given. Let x be the number of left-handed female students and let y be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be 5x and the number of right-handed male students will be 9y. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:

x+y=18

5x+9y=122

When you solve this system of equations, you get x=10 and y=8. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is 

50

122

, which to the nearest thousandth is 0.410.

The final answer is A.

Questions 8 & 9

Use the following information for both question 7 and question 8.

If shoppers enter a store at an average rate of r shoppers per minute and each stays in the store for average time of T minutes, the average number of shoppers in the store, N, at any one time is given by the formula N=rT. This relationship is known as Little's law.

The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little's law to estimate that there are 45 shoppers in the store at any time.

Question 8

Little's law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?

ANSWER EXPLANATION: Since the question states that Little's law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, N, in the checkout line at any time is N=rT, where r is the number of shoppers entering the checkout line per minute and T is the average number of minutes each shopper spends in the checkout line.

Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with T=5). Since there are 60 minutes in one hour, the rate is 

84shoppersperhour

60minutes

=1.4 shoppers per minute. Using the given formula with r=1.4 and T=5 yields

N=rt=(1.4)(5)=7

Therefore, the average number of shoppers, N, in the checkout line at any time during business hours is 7.

The final answer is 7.

Question 9

The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)

ANSWER EXPLANATION: According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little's law, there are, on average, N=rT=(1.5)(12)=18 shoppers in the new store at any time. This is

45−18

45

*100=60

percent less than the average number of shoppers in the original store at any time.

The final answer is 60.

Question 10

In the xy-plane, the point (p,r) lies on the line with equation y=x+b, where b is a constant. The point with coordinates (2p,5r) lies on the line with equation y=2x+b. If p≠0, what is the value of 

r

p

?

A) 

2

5

B) 

3

4

C) 

4

3

D) 

5

2

ANSWER EXPLANATION: Since the point (p,r) lies on the line with equation y=x+b, the point must satisfy the equation. Substituting p for x and r for y in the equation y=x+b gives r=p+b, or b = r−p.

Similarly, since the point (2p,5r) lies on the line with the equation y=2x+b, the point must satisfy the equation. Substituting 2p for x and 5r for y in the equation y=2x+b gives:

5r=2(2p)+b

5r=4p+b

b = 5r−4p.

Next, we can set the two equations equal to b equal to each other and simplify:

b=r−p=5r−4p

3p=4r

Finally, to find 

r

p

, we need to divide both sides of the equation by p and by 4:

3p=4r

3=

4r

p

3

4

=

r

p

The correct answer is B, 

3

4

.

If you picked choices A and D, you may have incorrectly formed your answer out of the coefficients in the point (2p,5r). If you picked Choice C, you may have confused r and p.

Note that while this is in the calculator section of the SAT, you absolutely do not need your calculator to solve it!

Question 11

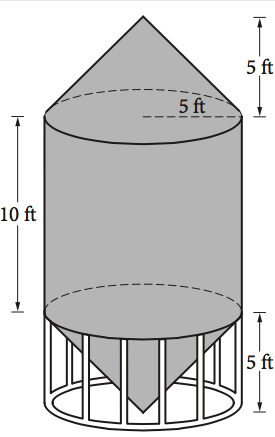A grain silo is built from two right circular cones and a right circular cylinder with internal measurements represented by the figure above. Of the following, which is closest to the volume of the grain silo, in cubic feet?

A) 261.8
B) 785.4
C) 916.3
D) 1047.2

ANSWER EXPLANATION: The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section:

Volume of a Cone

V=

1

3

πr2h

Volume of a Cylinder

V=πr2h

can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by

Vsilo=π(52)(10)+(2)(

1

3

)π(52)(5)=(

4

3

)(250)π

which is approximately equal to 1,047.2 cubic feet.

The final answer is D.

Question 12

If x is the average (arithmetic mean) of m and 9, y is the average of 2m and 15, and z is the average of 3m and 18, what is the average of x, y, and z in terms of m?

A) m+6
B) m+7
C) 2m+14
D) 3m+21

ANSWER EXPLANATION: Since the average (arithmetic mean) of two numbers is equal to the sum of the two numbers divided by 2, the equations x=

m+9

2

, y=

2m+15

2

, z=

3m+18

2

are true. The average of x, y, and z is given by 

x+y+z

3

. Substituting the expressions in m for each variable (x, y, z) gives

[ m+9 2 + 2m+15 2 + 3m+18 2 ]

3

This fraction can be simplified to m+7.

The final answer is B.

Question 13

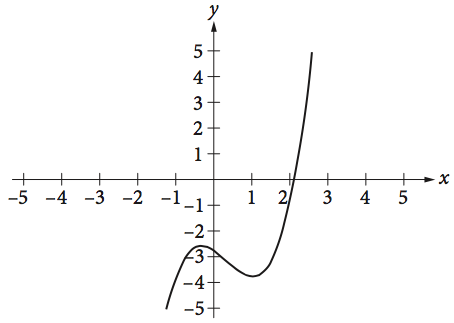
The function f(x)=x3−x2−x−

11

4

 is graphed in the xy-plane above. If k is a constant such that the equation f(x)=k has three real solutions, which of the following could be the value of k?

ANSWER EXPLANATION: The equation f(x)=k gives the solutions to the system of equations

y=f(x)=x3−x2−x−

11

4

and

y=k

A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the xy-plane.

The graph of y=k is a horizontal line that contains the point (0,k) and intersects the graph of the cubic equation three times (since it has three real solutions). Given the graph, the only horizontal line that would intersect the cubic equation three times is the line with the equation y=−3, or f(x)=−3. Therefore, k is −3.

The final answer is D.

Question 14

q=

1

2

nv2

The dynamic pressure q generated by a fluid moving with velocity v can be found using the formula above, where n is the constant density of the fluid. An aeronautical engineer users the formula to find the dynamic pressure of a fluid moving with velocity v and the same fluid moving with velocity 1.5v. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?

ANSWER EXPLANATION: To solve this problem, you need to set up to equations with variables. Let q1 be the dynamic pressure of the slower fluid moving with velocity v1, and let q2 be the dynamic pressure of the faster fluid moving with velocity v2. Then

v2=1.5v1

Given the equation q=

1

2

nv2, substituting the dynamic pressure and velocity of the faster fluid gives q2=

1

2

n(v2)2. Since v2=1.5v1, the expression 1.5v1 can be substituted for v2 in this equation, giving q2=

1

2

n(1.5v1)2. By squaring 1.5, you can rewrite the previous equation as

q2=(2.25)(

1

2

)n(v1)2=(2.25)q1

Therefore, the ratio of the dynamic pressure of the faster fluid is

q2

q1

=

2.25q1

q1

=2.25

The final answer is 2.25 or 9/4.

Question 15

For a polynomial p(x), the value of p(3) is −2. Which of the following must be true about p(x)?

A) x−5 is a factor of p(x).
B) x−2 is a factor of p(x).
C) x+2 is a factor of p(x).
D) The remainder when p(x) is divided by x−3 is −2.

ANSWER EXPLANATION: If the polynomial p(x) is divided by a polynomial of the form x+k (which accounts for all of the possible answer choices in this question), the result can be written as

p(x)

x+k

=q(x)+

r

x+k

where q(x) is a polynomial and r is the remainder. Since x+k is a degree-1 polynomial (meaning it only includes x1 and no higher exponents), the remainder is a real number.

Therefore, p(x) can be rewritten as p(x)=(x+k)q(x)+r, where r is a real number.

The question states that p(3)=−2, so it must be true that

−2=p(3)=(3+k)q(3)+r

Now we can plug in all the possible answers. If the answer is A, B, or C, r will be 0, while if the answer is D, r will be −2.

A. −2=p(3)=(3+(−5))q(3)+0
−2=(3−5)q(3)
−2=(−2)q(3)

This could be true, but only if q(3)=1

B. −2=p(3)=(3+(−2))q(3)+0
−2=(3−2)q(3)
−2=(−1)q(3)

This could be true, but only if q(3)=2

C. −2=p(3)=(3+2)q(3)+0
−2=(5)q(3)

This could be true, but only if q(3)=

−2

5

D. −2=p(3)=(3+(−3))q(3)+(−2)
−2=(3−3)q(3)+(−2)
−2=(0)q(3)+(−2)

This will always be true no matter what q(3) is.

Of the answer choices, the only one that must be true about p(x) is D, that the remainder when p(x) is divided by x−3 is -2.

The final answer is D.